The effectiveness of lenses is a measure of their ability to generate the light’s deviation. A lens with a shorter focal length will produce more dispersion of light than lenses with a longer focal length. Therefore, the strength of the lens can be defined as the ratio of its focal length to its reciprocal. S.I. the measure of the power of a lens is dioptre. It is indicated by the letter D.
In this article, let’s know about the power of lens and Lens Power Formula.
Power of Lens
The effectiveness of lenses is a measure of their capacity to create an inclination of light. A lens with a shorter focal length can produce more dispersion of light than lenses with a longer focal length. Therefore, the strength of the lens could be measured as the reciprocal of the focal length. The power unit of a lens is dioptre, which is the equivalent of meters.
Power of a lens,
P = 1/F
One diopter = P when the focal length is 1m. Thus, the power of one lens is 1D when it has a focal length greater than 1m. When multiple lenses have been in contact, their combined power is calculated as:
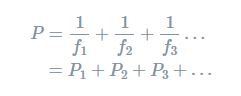
The right sign of one’s character must be considered when making calculations of the power. Positive power for convex lenses and negative in the case of concave lenses according to the sign that F’.
Given:
The focal length of the lens A,
(converted ‘m’ into ‘km’)
Lens B’s focal length,
(converted ‘m’ into ‘km’)
To discover nature and the power from each lens (A and B).
Solution:
- To determine the power for lens A.
- We know that the strength of the lens can be measured by:
![]()
- In the context of the expression above, we will get:
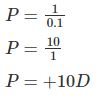
The power for lens A is 10D, and the plus sign indicates that it is either converging or convex.
Now,
- To calculate the power of the lens, B.
- We know that power of the lens is given as
![]()
- Putting the value of in the above expression, we get:
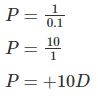
The strength of lens A is 10D, and the minus sign indicates that it is concave or diverging in nature.
When a lens is convex when the object is in the lens’s focus or between the optical centre and the focal point, the resultant image is always erect, virtual, and magnified. Concave lenses produce a vertical and virtual smaller image regardless of the object’s distance to the lens.
The object, in this case, is located 8 cm away from the lens, which is located at a distance that is less than its focal length. In this instance, the lens with the convex shape creates a virtual larger image magnified by the object.
Power of a Lens Formula
To calculate the power of the lens within Ray Optics, apply the power of lens formula.
P=1/F
If the focal distance of the lens is specified by meters (m), then the lens’s power is measured in diopters (D) which means that the power unit for this lens is called a diopter. Another thing to remember is that for a diverging lens, the optical power will be positive, while when it is a diverging lens, it’s negative.
For instance, If the lens’s focal length is 20 centimetres when converted to meters, we’ll get 0.2 millimetres. To determine the strength of this lens, you need to consider its reciprocal 0.2, and we will find 5. So, the capacity of this particular lens is 5D.
If you’ve read previously about the formula used by lens makers, you’ve realised what we’re calculating is the lens’s capacity. This means you can determine the power of a lens by using the radii of curvature between two surfaces, as well as an index for refractive properties of the lens’s material.
A primary application for the potential of lenses is Optometry”.
Optometrists recommend corrective lenses (either the convex lens or the concave lenses) by depreciating sight. Your eye is a lens, and you could be unable to maintain a clear sight at times. The solution is wearing corrective lenses that have the correct capacity.
Measuring Focal Length
Convex Lens
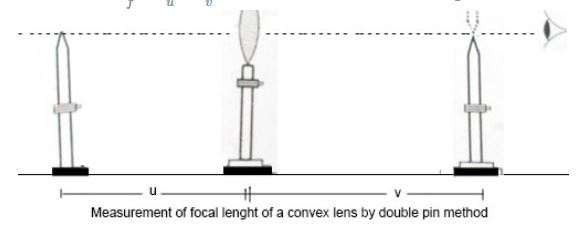
Convex lens focal length lens can be determined by using the u-v method. The approximate focal length of a convex lens can be measured by focusing an object of a distance on a wall or screen. This is called the distance that the lens has to the display.
The pin for the object can be placed on one end of the bench, at more than 2f in front of the lens. Further, you can position it on the opposite side of the bench. After that, the image of the object pin will be reversed, and the tip of the image will be positioned on top of the picture pin.
Distance is determined in determining the position of pins and the distance to the object and the image. Several distances are measured, and then using these numbers in the lens formula 1/f = 1/1 + 1/1
1f=1u + 1v can be calculated as the length of the lens.
Concave lens
A lens’s focal distance of the concave lens may be measured using a convex lens. A convex lens M with the known length of its focus is placed on an optical bench. On one end of the bench, the object pin that is more from the focal length of M is fixed, and the exact location of the image is located at O, as seen in the figure. In the second figure, a third pin has been fixed.
Then, between the pin O and M image, the concave lens is placed on a stand. Since the light beam converging has been reflected upon the concave lens, O becomes an actual object.
Since the concave lens diverts the light rays, an image is formed when I is away from the lenses. Pins are fixed at I, and their location is determined after removing the parallax separating the two pins at O and I.
After determining the positions between M, O, and I, the distance between O.L. and I.L. can be determined. Thus, object distance, u = L.O., and image distance, the v value is LI. By adding the values of v and u together, we can determine the value of the focal length of the lens concave.
Conclusion
Many of us wear glasses, and we know that it has specific numbers (in plus and minus). In the same way, there are many convex and concave lenses around us. Did we observe it differently today, didn’t we? Calculating the power of the lens doesn’t include deep maths, and that’s good news.

Leave a Reply